Matematikte bölme, bir sayının başka bir sayıya bölünmesi işlemidir ve sonuç bölen sayının bölünen sayı içinde kaç kez olduğunu ifade eder.
Bölme İşlemi
e, d,u,n,e,t,t,e birer doğal sayı
ve d ≠ 0 olmak üzere e sayısının b sayısına bölünmesi ile elde edilen bölüm u ve kalan t ise;
e= d x u + t dir.
Örneğin;
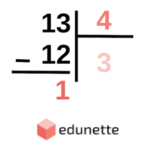
Bölünen: 13, Bölen: 4, Bölüm: 3 Kalan: 1 ‘ dir.
Not: Bölme işleminde kalan bölenden küçük olmak zorundadır.
( 0 ≤ K < B )
Bölünebilme Kuralları
Matematikte bölünebilme, bir sayının başka bir sayıya tam olarak bölünebilmesi durumunu ifade eder.
2 ile Bölünebilme Kuralı
Birler basamağında 0, 2, 4, 6, 8 olan sayı olan yani birler basamağında çift sayılardan biri var ise 2 ile kalansız (tam) bölünebilir.
3 ile Bölünebilme Kuralı
Verilen bir sayının 3 ile tam olarak bölünebilmesi için rakamlarının toplamı 3 veya 3’ün katı olmalıdır.
4 İle Bölünebilme Kuralı
Verilen bir sayının 4 ile tam bölünebilmesi için son iki basamağının 4’e tam bölünmesi gerekir.
- edu sayısının 4 ile bölümünden kalan ut’ nin (son iki basamak) 4 ile bölümünden kalana eşittir.
edu sayısının 4 ile bölümünden kalan u+ 2 . d nin 4 ile bölümünden kalana eşittir.
5 İle Bölünebilme Kuralı
Verilen bir sayının 5 ile tam olarak bölünebilmesi için son basamağının 0 ve ya 5 olması gerekir.
Not: Bir sayının 5 ile bölümünden kalan, o sayının birler basamağındaki rakamın 5 ile bölümünden kalana eşittir.
6 İle Bölünebilme Kuralı
Verilen bir sayının 6 ile tam bölünebilmesi için hem 2 hem de 3 ile tam bölünmesi gerekir.
Not: 6 ile bölünebilmede de görüldüğü gibi verilen bir sayının istenen sayıya tam olarak bölünebilmesi için bu sayıyı oluşturan aralarında asal sayılara da bölünmesi gerekir. Aralarında asal sayıların çarpımına da tam olarak bölünmesi gerekir.
7 İle Bölünebilme Kuralı
(n + 1) basamaklı anan-1 … a4a3a2a1a0 sayısının 7 ile tam bölünebilmesi için,
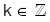
Olmak üzere, (a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) +…– … = 7k olmalıdır.
8 İle Bölünebilme Kuralı
Verilen bir sayının 8 ile tam bölünebilmesi içim son 3 basamağının 8 ile tam olarak bölünmesi gerekir.
4000, 3432, 84104 sayıları 8 ile tam bölünür.
Birler basamağı u, onlar basamağı d, yüzler basamağı e, … olan sayının
(… edu sayısının) 8 ile bölümünden kalan u + 2 × d+ 4 × e toplamının 8 ile bölümünden kalana eşittir.
9 İle Bölünebilme Kuralı
Bölünmesi istenen sayının rakamları toplamı 9 ve 9’un katı ise bu sayı 9’a tam bölünür. Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalana eşittir.
10 ile Bölünebilme Kuralı
Verilen bir sayının 10 ile tam olarak bölünebilmesi için son basamağının “0” olması gerekir. Bir sayının birler basamağındaki rakam o sayının 10 ile bölümünden kalandır.
11 ile Bölünebilme Kuralı
(n + 1) basamaklı anan–1 … a4a3a2a1a0 sayısının 11 ile tam bölünebilmesi için(a0 + a2 + a4 + …) – (a1 + a3 + a5 + …)… = 11 . k ve
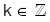
olmalıdır.
(a0 + a2 + a4 + …) – (a1 + a3 + a5 + …)… işleminin sonucunun 11 ile bölümünden kalana eşittir.