Rakam Nedir? Sayı Nedir?
Sayıları ifade etmeye yarayan sembollere rakam denir. Örneğin; 0,1,2,3,4,5,6,7 Rakamların çokluk belirtecek şekilde bir araya getirilmesiyle oluşturulan ifadeler ifadesine sayı denir.
- Sayma Sayıları
1,2,3,4,5,6,7,8… N sayı kümesinin her bir elemanına “sayma sayıları” denir.
- Doğal Sayılar
0,1,2,3,4,5,6,7 sayı kümesinin tamamı doğal sayı olarak kabul edilmektedir.
- Tam Sayılar
(-n…….-3,-2,-1,0,1,2,3,4….. ) Z – sonsuzdan başlayarak + sonsuza kadar uzanan sayı kümelerine “tam sayılar” denir.
Tam sayılar kümesi; negatif tam sayılar kümesi: ![]()
şeklinde, pozitif tam sayılar kümesi : ![]()
Buna göre,
![]() dır.
dır.
- Rasyonel Sayılar
e ve d aralarında asal tam sayı ve d≠0
e/d olarak yazılabilen tüm sayıların oluşturduğu kümeye rasyonel sayı denir.
- İrrasyonel Sayılar
E ve d aralarında asal tam sayılar ve d sıfırdan farklı olmak üzere e/d şeklinde yazılamayan sayıların kümesine irrasyonel sayılar kümesi denir ve ”Q“ harfi ile isimlendirilir.
*Kök dışına tam olarak çıkamayan sayılar irrasyonel sayıdır.
*Ondalık açılımı sınırsız ve devirsiz olan sayılar irrasyonel sayıdır.
- Tek ve Çift Sayılar
T= Tek Sayı Ç=Çift Sayı olmak üzere;
- İki çift sayının toplamı ve farkı her zaman çift sayıdır.
Ç+Ç=Ç Ç-Ç=Ç
2+2=4 6-4=2
- İki tek tam sayının toplamı ve farkı her zaman çift sayıdır.
T+T= Ç T-T=Ç
5+3=8 9-5=4
- Bir çift tam sayı ile bir tek tam sayının toplamı ve farkı her zaman tek tam sayıdır.
T + Ç = T, T- Ç= T dir.
- İki veya daha fazla tam sayıdan en az biri çift tam sayı ise çarpımları her zaman çift tam sayıdır.
ÇxÇ=Ç
TxÇ=Ç
- İki veya daha fazla tek tam sayının çarpımı her zaman tek tam sayıdır.
TxT = T dir.
- Tek tam sayıların veya çift tam sayıların bölümü için kesin yargılarda bulunulamaz.
- Tek veya çift olma, tam sayılar için geçerlidir.
- Rasyonel sayılara tek veya çift sayı denemez.
Not: Çift sayıların kuvveti pozitif tam sayı olmalıdır. Çift sayıların kuvveti sıfır veya negatif olursa ifade çift sayı belirtmez.
- Pozitif ve Negatif Sayılar
Sıfırdan küçük sayılara negatif sayılar denir. e negatif sayı ise “e < 0” şeklinde gösterilir.
Sıfırdan büyük sayılara pozitif sayılar denir. d pozitif sayı ise “d > 0” şeklinde gösterilir.
“0” pozitif veya negatif sayı değildir.
- Pozitif sayıların toplamı daima pozitiftir.
e>0 d>0 e+d>0
- Negatif Sayıların toplamı daima negatiftir.
e<0 d<0 e+d<0
- Zıt işaretli sayıların toplamı için kesin bir yargıda bulunulamaz. Sonuç, sayısal değerce büyük olanın işaretini alır.
e+d<0, e+d>0,e+d=0 e>0 y>0
- Aynı işaretli iki sayının çarpımı veya bölümü daima pozitiftir.
e>0 d>0 exd>0 e/d>0
- Pozitif sayıların bütün kuvvetleri pozitiftir. n bir tam sayı x pozitif sayı olmak üzere daima pozitiftir.
- Ardışık Sayılar
- Belirli bir kurala göre art arda gelen sayı dizilerine ardışık sayılar denir.
e bir tam sayı olmak üzere,
- Ardışık dört tam sayı sırasıyla;
e, e+1, e+2, e+3 tür.
- Ardışık dört çift sayı sırasıyla;
2e, 2e + 2, 2e + 4, 2e + 6’dır.
- Ardışık dört tek sayı sırasıyla;
2e+1, 2e+3, 2e+5, 2e+7 dir.
- Üçün katı olan ardışık dört tam sayı sırasıyla;
3e, 3e+3, 3e+6, 3e+9 dur.
Bazı Ardışık Sayıların Toplamı e bir sayısı olmak üzere;
- Ardışık sayma sayılarının toplamı
1+2+3+4+…………………+e = e(e+1)/2 formülü ile hesaplanmaktadır.
- Ardışık pozitif çift doğal sayıların toplamı ise
2 + 4 + 6 + … + (2e) = e(e+1)
- Ardışık tek doğal sayıların toplamı
1 + 3 + 5 + … + (2e–1) = e2
- Artış miktarı eşit olan ardışık tam sayıların toplamı
- Terim Sayısı
Terim Sayısı = [(Son Terim – İlk Terim) / Artış Miktarı] + 1
r : İlk terim
n : Son terim
x : Artış miktarı olmak üzere,
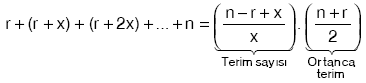
şeklinde olur.
9. Asal Sayı
1 ve kendisinden başka pozitif böleni olmayan 1’den büyük doğal sayılara asal sayı denir. Asal sayılar; 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, … şeklinde sıralanır.
- En küçük asal sayı 2’dir.
- 1 asal sayı değildir.
- Negatif sayılar asal sayı değildir.
- 2 dışında çift olup aynı zamanda asal olan başka bir sayı yoktur.
Aralarında Asal Sayılar
1’den başka pozitif ortak böleni olmayan iki veya daha fazla sayıya aralarında asal sayı denir.
Ardışık sayılar daima aralarında asaldır.
1 bütün pozitif tam sayılarla aralarında asaldır.
10. Faktöriyel
1’den n doğal sayısına kadar olan doğal sayıların çarpımına faktöriyel denir ve n! İle gösterilir.
n! = n.(n-1).(n-2)…3.2.1
0! = 1
1! = 1
2! = 2.1
3!=3.2.1
10!=10.9.8.7!
15!= 15.14.13!
n!=n.(n-1).(n-2)!
Matematik en iyi ve en kalıcı şekilde Edunette birebir online özel matematik dersleri ile öğrenilir. Edunette web sitesini ziyaret edip, istediğiniz öğretmeni seçerek ücretsiz deneme dersi alabilirsiniz.
İlginizi Çekebilir : Birinci ve İkinci Derecede Denklemler Konu Anlatımı



