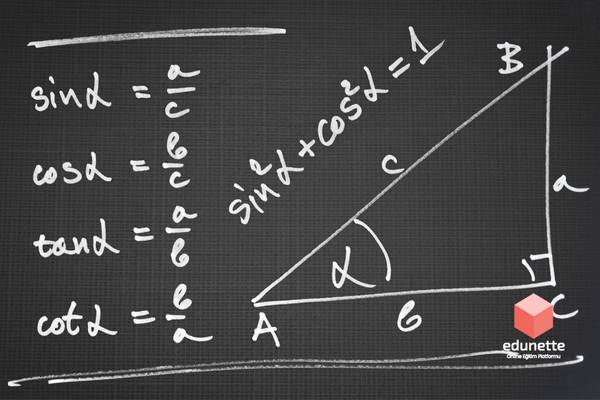
Trigonometri, matematikte açıları, üçgenleri ve bu üçgenlerin kenarları arasındaki ilişkileri inceler. AYT sınavında trigonometri konusu oldukça önemlidir ve bu nedenle, konu hakkında sağlam bir anlayışa sahip olmanız gerekir.
Trigonometri konusu, üç ana alt konuya ayrılır: açıların ölçüsü, trigonometrik oranlar ve trigonometrik fonksiyonlar. Şimdi sırayla bu konulara değineceğim:
Açıların ölçüsü:
Açıların ölçüsü, genellikle derece veya radyan cinsinden ifade edilir. Derece, bir tam açının 360 eşit parçaya bölündüğü birimdir. Radyan ise, birim çemberin merkez açı ölçüsüdür. Bir tam açı, 2π radyana eşittir.
Trigonometrik oranlar:
Trigonometrik oranlar, bir üçgenin iç açıları ve kenarları arasındaki ilişkileri ifade eder. Üçgenin iç açıları, toplamda 180 derece veya π radyan ölçüsüne sahiptir.
Trigonometrik oranlar;
sin(θ) = karşı kenar / hipotenüs
cos(θ) = bitişik kenar / hipotenüs
tan(θ) = karşı kenar / bitişik kenar
Burada θ, açının ölçüsüdür. Hipotenüs, üçgenin en uzun kenarıdır ve karşı kenar, açının karşısındaki kenarı, bitişik kenar ise açının yanındaki kenarı ifade eder.
Trigonometrik fonksiyonlar:
Trigonometrik fonksiyonlar, sinüs, kosinüs ve tanjant fonksiyonlarını ifade eder. Bu fonksiyonlar, açının ölçüsüne göre karşı kenar, bitişik kenar ve hipotenüs arasındaki oranları ifade eder.
sin(θ) = karşı kenar / hipotenüs
cos(θ) = bitişik kenar / hipotenüs
tan(θ) = karşı kenar / bitişik kenar
Bu fonksiyonların tersleri de vardır:
sin⁻¹(x) = θ
cos⁻¹(x) = θ
tan⁻¹(x) = θ
Burada x, sin, cos veya tan fonksiyonlarına göre bir oranı ifade eder ve θ, bu orana karşılık gelen açının ölçüsüdür.
Trigonometri Soru Çözümleri
30 derecelik bir açının karşısındaki kenarın uzunluğu 5 cm olarak verildiğine göre, hipotenüsün uzunluğunu bulmak için trigonometrik oranlardan yararlanabiliriz.
Öncelikle, bu üçgenin hipotenüsü ve bitişik kenarı arasındaki oranı ifade eden cos fonksiyonunu kullanalım:
cos(30°) = bitişik kenar / hipotenüs
30 derecelik açının cosinüs değeri, trigonometrik tablolardan ya da hesap makinesi kullanarak bulunabilir. Bu değer yaklaşık 0,866’dır.
Yani, 0,866 = bitişik kenar / hipotenüs
Bitişik kenarın uzunluğu bize verilmediği için, burada bilinmeyen bir değişkenimiz var. Ancak, bu değişkeni bulmak için verilen bilgileri kullanabiliriz.
Verilen bilgiye göre, açının karşısındaki kenarın uzunluğu 5 cm olduğuna göre, sin fonksiyonunu kullanarak bitişik kenarın uzunluğunu bulabiliriz:
sin(30°) = karşı kenar / hipotenüs
sin(30°) = 5 / hipotenüs
hipotenüs = 5 / sin(30°)
sin(30°) değeri yaklaşık 0,5 olduğundan, hipotenüsün uzunluğu şöyle hesaplanabilir:
hipotenüs = 5 / 0,5 = 10 cm
Böylece, hipotenüsün uzunluğunun 10 cm olduğunu bulduk.
Bir üçgenin açıları sırasıyla 30°, 60° ve 90° ise, hipotenüsün uzunluğu nedir?
30-60-90 üçgeni olarak adlandırılan bu üçgenin özellikleri, trigonometrik oranlardan yararlanarak kolayca bulunabilir.
Öncelikle, üçgenin en uzun kenarı olan hipotenüsün uzunluğunu bulalım. Hipotenüs, üçgenin 90 derecelik açısına karşılık gelen kenardır.
Sin fonksiyonunu kullanarak, karşı kenarın uzunluğunu hesaplayabiliriz:
sin(60°) = karşı kenar / hipotenüs
sin(60°) = (√3) / 2
Karşı kenar, hipotenüsün yarısıdır, yani:
karşı kenar = (hipotenüs) / 2
Böylece, hipotenüsün uzunluğunu şöyle hesaplayabiliriz:
(√3) / 2 = karşı kenar / hipotenüs
hipotenüs = karşı kenar / ((√3) / 2)
hipotenüs = (hipotenüs / 2) / ((√3) / 2)
hipotenüs = hipotenüs / (√3)
İki tarafı da (√3) ile çarp; hipotenüs * (√3) / 2 = karşı kenar
Burada, hipotenüsün uzunluğunu bilmediğimiz için, bilinmeyen bir değişken olarak belirleyebiliriz. Diyelim ki hipotenüsün uzunluğu x olsun. Böylece:
x * (√3) / 2 = x / 2 * karşı kenar = x / 2
Buradan, hipotenüsün uzunluğunu şu şekilde hesaplayabiliriz:
x * (√3) / 2 = x / 2
2x * (√3) / 2 = x
x * (√3) = x
x = x / (√3)
Yani, hipotenüsün uzunluğu karşı kenarın uzunluğunun (√3) katıdır:
hipotenüs = (√3) * karşı kenar
Karşı kenar, 30 derecelik açıya karşılık gelen kenardır. Tan fonksiyonunu kullanarak, karşı kenarın uzunluğunu hesaplayabiliriz:
tan(30°) = karşı kenar / bitişik kenar
tan(30°) = (√3) / 1
Böylece, karşı kenarın uzunluğu (√3) birimdir.
Sonuç olarak, hipotenüsün uzunluğu (√3) * (√3) = 3 birimdir.
Örnek 2
Bir üçgenin bir açısı 60 derece ve karşı kenarının uzunluğu 8 birim ise, hipotenüs ve diğer kenarın uzunluğunu bulunuz.
Bu üçgenin bir açısı 60 derece olduğuna göre, diğer açıları 60 derece ve 60 derece olacaktır. Karşı kenarın uzunluğu 8 birim olduğuna göre, diğer kenarların uzunluğu ne olabilir?
İlk önce, karşı kenarın uzunluğu ile ilgili bilgileri kullanarak, trigonometri fonksiyonlarından biri ile diğer kenarın uzunluğunu hesaplayabiliriz. Bu durumda, tan fonksiyonunu kullanabiliriz:
tan(60°) = karşı kenar / bitişik kenar
tan(60°) = (√3) / bitişik kenar
bitişik kenar = (√3) / tan(60°)
bitişik kenar = (√3) / (√3) = 1 birim
Şimdi, diğer kenarın uzunluğunu hipotenüs olarak belirleyebiliriz ve Pythagoras teoremine göre hesaplayabiliriz:
hipotenüs^2 = karşı kenar^2 + bitişik kenar^2
hipotenüs^2 = 8^2 + 1^2
hipotenüs^2 = 65
hipotenüs = √65 birim
Böylece, hipotenüsün uzunluğu √65 birim, diğer kenarın uzunluğu 1 birimdir.
Birebir online özel matematik dersi almak için Edunette web sitesini ziyaret ederek istediğiniz öğretmeni seçin ve ücretsiz deneme dersi alarak hemen başlayın!